movie The movie is in .mov format; about 10 Mbyte.
A movie of the algorithm running can be helpful in understanding how it works. This movie comes from joint work between myself and Paul Bourke, with my data and Paul's movie-making.
These annular rings have an inner diameter which is 2/3 of the outer diameter, and illustrate how the algorithm runs with a hollow shape. They are shown with heirarchical color. A property called rank is assigned, such that if a ring does not contain any smaller rings it has rank 0. If the highest-rank ring within a given ring has rank k, that ring is assigned rank k+1. Each rank has a unique color. The populations of the ranks are:
rank 7 - 1
rank 6 - 4
rank 5 - 10
rank 4 - 20
rank 3 - 41
rank 2 - 81
rank 1 -189
rank 0 - 355
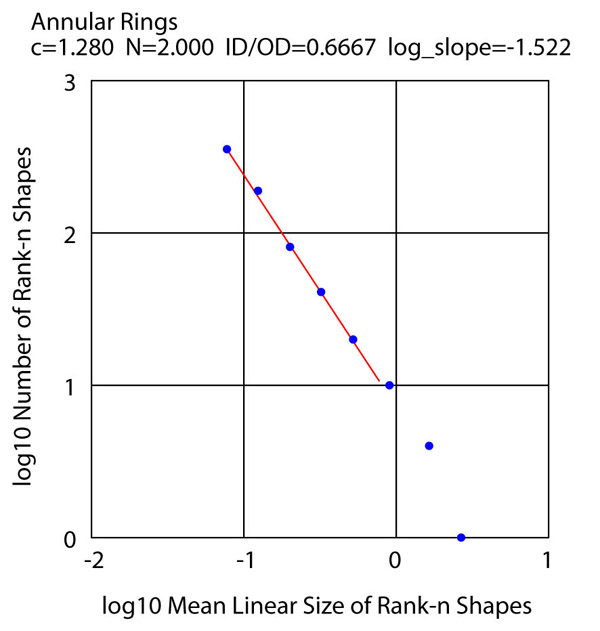
The chart gives a log-log plot of the population of each rank versus the mean ring linear dimension for the given rank. The data is close to a straight line, indicating that the ring rank populations obey a negative-exponent power law with negative exponent value approximately 1.52. The rank populations thus have a statistical distribution which many would call "fractal".

One object was to demonstrate the space-filling property. To this end a c value close to the upper limit was used, resulting in a final image with 82% fill. A total of 27,264,622 trials were made to place 701 squares, for an average of about 39,000 trials per placement. c=1.28, N=2, fractal D=1.56. It can be seen that any available space receives a ring just as soon as the next-ring diameter is small enough to go into it.
A mathematical account of the algorithm is given in the Shier-Bourke paper in Computer Graphics Forum: paper